NOR 게이트
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
NOR 게이트는 두 개 이상의 입력 중 하나라도 높으면(1) 출력이 낮아지고(0), 모든 입력이 낮으면(0) 출력이 높아지는(1) 디지털 논리 게이트이다. NOR 게이트는 미국(ANSI/MIL), IEC, DIN의 세 가지 기호로 표현되며, ANSI 기호는 반전 버블이 있는 OR 게이트이다. NOR 게이트는 TTL 및 CMOS IC에서 널리 사용되며, 4001과 같은 표준 CMOS IC에는 여러 개의 독립적인 2입력 NOR 게이트가 포함되어 있다. 또한 NOR 게이트는 NAND 게이트와 함께 기능적 완전성을 가지며, 다른 모든 논리 함수를 구현하는 데 사용될 수 있다.
더 읽어볼만한 페이지
| NOR 게이트 | |
|---|---|
| 기본 정보 | |
 | |
 | |
| 설명 | 논리곱 부정 (Not OR) |
| 기능 | 두 입력 중 하나 또는 모두 거짓일 때 참을 출력 |
| 진리표 | 아래 참조 |
| 추가 정보 | |
| 입력 | 2개 이상 |
| 출력 | 1개 |
| 유형 | 디지털 논리 |
| 구현 | 다이오드-트랜지스터 논리 (DTL), 트랜지스터-트랜지스터 논리 (TTL), 상보형 금속 산화막 반도체 (CMOS) |
| 관련 항목 | 논리 회로, AND 게이트, OR 게이트, NAND 게이트, XOR 게이트, XNOR 게이트, 불 대수 |
2. 기호
NOR 게이트는 여러 표준 기호를 사용하여 표현된다. 논리 회로 문서에서 더 자세한 정보를 확인할 수 있다. NOR 게이트의 ANSI 기호는 OR 게이트에 도치 버블(inversion bubble)이 연결된 형태이며, 버블은 OR 게이트의 기능이 반전되었음을 나타낸다.
 |  | |
| MIL/ANSI 기호 | IEC 기호 | DIN 기호 |
2. 1. ANSI/MIL 기호
미국 표준 협회(ANSI) 및 군사 표준에서 사용하는 기호는 OR 게이트 모양에 출력 쪽에 작은 원(반전)이 붙은 형태이다.
2. 2. IEC 기호
국제전기기술위원회(IEC)에서 사용하는 기호는 직사각형 모양에 OR 게이트를 나타내는 ">=1" 기호와 출력 쪽에 작은 원(반전)이 붙은 형태이다.
2. 3. DIN 기호
DIN 기호는 현재는 잘 사용되지 않지만, OR 게이트를 나타내는 곡선 모양에 출력 쪽에 작은 원(반전)이 붙은 형태이다.3. 하드웨어 설명 및 핀 배치
NOR 게이트는 트랜지스터-트랜지스터 논리(TTL) 및 CMOS 집적 회로(IC)로 구현된다. NOR는 범용 로직 IC에서 NAND 다음으로 기본적인 제품으로, 74 시리즈의 경우 TTL 7402 외에도 74HC02 등 CMOS 버전 등 많은 변형이 있다.
74 시리즈와 4000 시리즈(CMOS)에서 다양한 NOR 게이트 IC를 사용할 수 있다.
- 74 시리즈 (TTL)
- 7402: 2입력 NOR 게이트 × 4
- 7427: 3입력 NOR 게이트 × 3
- 7425: 4입력 NOR 게이트 × 2
- 74260: 5입력 NOR 게이트 × 2
- 744078: 8입력 NOR 게이트 × 1
- 4000 시리즈 (CMOS)
- 4001: 2입력 NOR 게이트 × 4
- 4025: 3입력 NOR 게이트 × 3
- 4002: 4입력 NOR 게이트 × 2
- 4078: 8입력 NOR 게이트 × 1
더욱 오래된 RTL이나 ECL 방식에서는 NOR 게이트가 효율적이었기 때문에 많이 사용되었다.
3. 1. TTL 및 CMOS IC
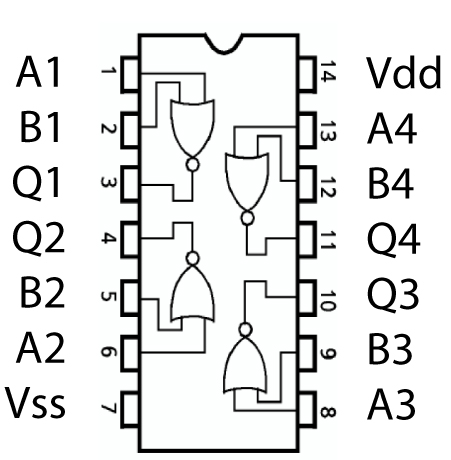
표준 4000 시리즈 CMOS IC인 4001은 4개의 독립적인 2입력 NOR 게이트를 포함한다. 핀 배열은 다음과 같다.{| class="wikitable"
|-
|
|-
|
| 핀 번호 | 기능 |
|---|---|
| 1 | 입력 A1 |
| 2 | 입력 B1 |
| 3 | 출력 Q1 |
| 4 | 출력 Q2 |
| 5 | 입력 B2 |
| 6 | 입력 A2 |
| 7 | Vss |
| 8 | 입력 A3 |
| 9 | 입력 B3 |
| 10 | 출력 Q3 |
| 11 | 출력 Q4 |
| 12 | 입력 B4 |
| 13 | 입력 A4 |
| 14 | Vdd |
|}
이 장치들은 페어차일드 반도체, 필립스, 텍사스 인스트루먼트와 같은 대부분의 반도체 제조업체에서 구할 수 있다. 일반적으로 스루홀 DIP 및 SOIC 형식으로 제공된다. 데이터시트는 대부분의 데이터시트 데이터베이스에서 쉽게 찾을 수 있다.
CMOS 및 TTL 논리 계열에서 최대 8개의 입력을 갖춘 NOR 게이트를 사용할 수 있다.[1]
| CMOS | TTL |
|---|---|
74 시리즈의 경우 TTL 7402 외에도 74HC02 등 CMOS 버전 등 많은 변형이 있다.
오래된 RTL 및 ECL 계열에서는 NOR 게이트가 효율적이고 널리 사용되었다.[2]
3. 2. 핀 배치
표준 4000 시리즈 CMOS IC인 4001은 4개의 독립적인 2입력 NOR 게이트를 포함한다. 4001 IC의 핀 배치는 다음과 같다.| 핀 번호 | 기능 |
|---|---|
| 1 | 입력 A1 |
| 2 | 입력 B1 |
| 3 | 출력 Q1 |
| 4 | 출력 Q2 |
| 5 | 입력 B2 |
| 6 | 입력 A2 |
| 7 | Vss |
| 8 | 입력 A3 |
| 9 | 입력 B3 |
| 10 | 출력 Q3 |
| 11 | 출력 Q4 |
| 12 | 입력 B4 |
| 13 | 입력 A4 |
| 14 | Vdd |
4. 구현
NOR 게이트는 NMOS 논리 회로, PMOS 논리 회로, CMOS 등 다양한 기술을 사용하여 구현할 수 있다.
| NMOS 논리 회로 | PMOS 논리 회로 | CMOS |
|---|---|---|
 |  |  |
NMOS 논리 회로는 입력 중 하나라도 높으면 해당 N 채널 MOSFET이 켜져 출력이 낮아지고, 그렇지 않으면 풀업 저항을 통해 출력이 높아진다. CMOS 회로는 풀업 저항 대신 P 채널 MOSFET을 사용하며, 입력에 다이오드와 저항을 추가하여 정전기 방전으로부터 소자를 보호한다. CMOS 회로에서는 NAND 게이트가 NOR 게이트보다 효율성이 더 높은데, 이는 n-MOSFET의 전하 이동성이 p-MOSFET보다 빠르기 때문이다.
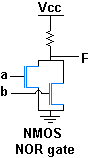
4. 1. NMOS 논리 회로
위의 그림은 NMOS 논리 회로를 사용하는 2입력 NOR 게이트의 구성을 보여준다. 입력 중 하나라도 높으면(HIGH, 1) 해당 N 채널 MOSFET이 켜지고 출력이 낮아진다(LOW, 0). 그렇지 않으면 출력은 풀업 저항을 통해 높아진다(HIGH, 1).[1]
4. 2. CMOS 논리 회로
CMOS 기술을 사용하는 경우, 풀업 저항 대신 P 채널 MOSFET을 사용하여 더 효율적인 회로를 구성한다. 입력에 다이오드와 저항을 추가하여 정전기 방전으로부터 소자를 보호한다.[1]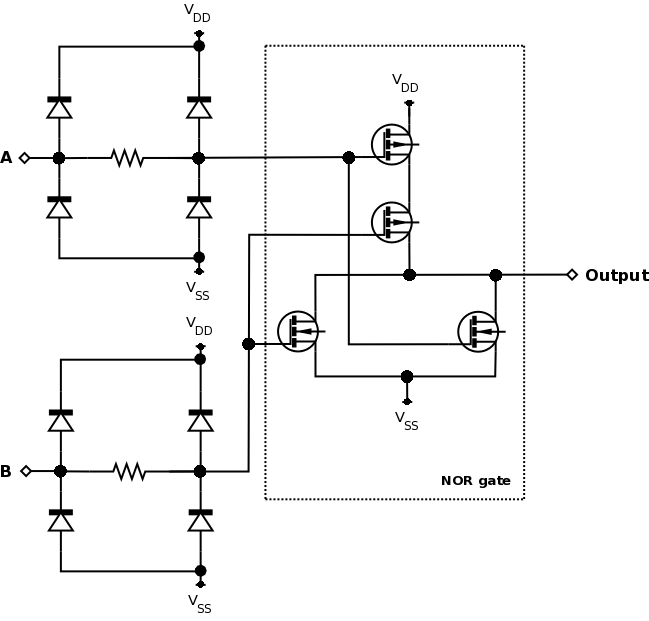
CMOS 회로에서는 NAND 게이트가 NOR 게이트보다 효율성이 더 높다. 이는 n-MOSFET의 전하 이동성이 p-MOSFET보다 빠르기 때문이며, NAND 게이트에서 p-MOSFET이 병렬로 연결되는 반면, NOR 게이트에서는 직렬로 연결되어 속도 저하가 발생하기 때문이다.[1]
5. 기능적 완전성
NOR 게이트는 NAND 게이트와 함께 기능적 완전성을 가진다. 즉, NOR 게이트만으로 다른 모든 논리 함수 (AND, OR, NOT 등)를 구현할 수 있다.[2]
NAND와 NOR 게이트는 유니버설 게이트(universal gate)로 간주되는데, 이는 다른 모든 게이트를 만드는데 사용될 수 있다는 것을 의미한다.[4] 따라서, 특정 NOR 게이트를 사용할 수 없는 경우에는 NAND 게이트로 부터 NOR 게이트를 만들 수 있다.
| 원하는 게이트 | NAND 구성 |
|---|---|
5. 1. NOR 게이트를 이용한 다른 게이트 구현
NOR 논리는 NAND 게이트와 마찬가지로 기능적 완전성을 갖는다. 즉, NOR 게이트만으로 다른 모든 논리 함수(AND, OR 등)를 구현할 수 있다.[2] 실제로 최초의 아폴로 유도 컴퓨터는 4,100개의 집적 회로(IC)를 사용했으며, 각 IC는 3개의 입력 NOR 게이트 2개만 포함하고 있었다.[3] 이처럼 NOR 게이트만으로도 전체 프로세서를 만들 수 있다.NAND 게이트 역시 기능적으로 완전하므로, NOR 게이트를 구할 수 없는 경우에는 NAND 게이트를 사용하여 NOR 게이트를 대체할 수 있다.[2] 아래 그림은 NAND 게이트만으로 NOR 게이트를 구성한 예시와, NOR 게이트만으로 NAND 게이트를 구성한 예시를 보여준다.
6. 응용
NOR 게이트는 NAND 게이트와 마찬가지로 기능적 완전성을 갖는다. 즉, NOR 게이트만으로 다른 모든 논리 함수(AND, OR 등)를 구현할 수 있다.[2] 예를 들어, 최초의 아폴로 유도 컴퓨터는 NOR 게이트만으로 구성된 4,100개의 집적 회로(IC)를 사용했다.[3]
만약 특정 NOR 게이트를 사용할 수 없는 경우, NAND 게이트 역시 기능적으로 완전하므로, NAND 게이트를 사용하여 NAND 논리로 NOR 게이트를 만들 수 있다.[2]
참조
[1]
웹사이트
Digital circuits, sizing, output impedance, rise and fall time.
https://inst.eecs.be[...]
[2]
서적
Logic and Computer Design Fundamentals, Third Edition.
Prentice Hall
[3]
서적
First-Hand:Hacking Apollo's Guidance Computer
https://ethw.org/Fir[...]
Engineering and Technology History Wiki
[4]
문서
Logic and Computer Design Fundamentals, Third Edition.
Prentice Hall
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
